(From the archive of ”bulk solids handling", article published in Vol. 32 (2012) No. 3 , ©2012 bulk-online.com)
1. Indentation Rolling Resistance and Belt Conveyor Design
The scale of modern belt conveyors requires that designs be predictive and analytical. It is generally agreed that indentation of the rubber belt cover as it passes over an idler can be a primary source of power loss in driving a belt conveyor system. This is particularly the case for long horizontal belt conveyors.

Understanding the role of various belt compounds and construction allows their associated parameters to be considered design variables for power and belt tension reduction and management. Varying operating environments and conveyor parameters also adds another level of complexity to the selection of the belt and other components in a conveyor system. Prediction of the energy loss due to indentation rolling resistance involves two modelling efforts:
- How rubber behaves under transient loading.
- How conveyor idler rolls indent the belt covers.
While several prediction methodologies have been developed over the years, recent modelling efforts have identified the importance of including the strain dependency of common belt cover rubbers in indentation rolling resistance predictions. This article compares the results of strain dependent analysis for a common rubber with laboratory test measurements of a conveyor belt running with the same covers.
1.1 Scope
The scope of this study was to examine a typical backing material to determine the major sources of error and variability in the steps required to make an indentation rolling resistance prediction and to draw conclusions about the accuracy of a predictive method by comparing results to direct measurements. In the process, various improvements to the published predictive methods were made. These and the effect of rubber test methods are organized in separate papers. The results from two direct tests – one a simple table top measurement, the other a full-scale test of a short belt segment – are provided for comparison to the current state of the calculations.
1.2 Material Properties and Characterisation
Modelling of the rubber begins with laboratory tests to determine the material strain/response behaviour over a range of temperatures and speeds or frequencies. For polymers and various dissipative materials like rubber compounds, such measurements are typically done with an oscillatory load versus strain instrument and there are standard, commercial DMA (Dynamic Mechanical Analyser) machines available for this purpose.The stiffness and recovery parameters of the rubbers used for conveyor belt covers are viscoelastic, i.e., vary with time and temperature. Typical modern DMA instruments process the raw, harmonic deformation and force reaction data at various controlled temperatures into frequency dependent storage and loss moduli, E' or E'', for a direct test (alternately G' or G'' for a shear mode test).These frequency and temperature dependent data are then overlain to form the classic ‘master curve’ for the material by assuming an analytical form of the time/temperature superposition principle of linear viscoelasticity such as given by the WLF (Williams, Landel, Ferry) law [cf. ref. 1]. The moduli are also often used directly in the ratio tan(δ) ≡ E''/E' = G''/G', called "tan delta". These moduli characterise assumedly linear viscoelastic materials, such that they depend only on frequency/temperature but are independent of strain levels.This linear behaviour for typical filled rubber compounds as used for belt backing material is found to be valid over only small strain ranges, or the magnitude E' and E'' can vary significantly with the impressed strain magnitude; typically less than about 0.1 percent. Carry loads on the idler rolls are often found to indent the backing well beyond the linear response range and has been demonstrated to have a significant effect on indentation loss prediction [2].A correction for strain used in this work, as in [2], has been a simple scaling of E' and E'' or G' and G'' to strain magnitude. This is an approximate correction since frequency and therefore temperature have some influence on strain sensitivity which varies with rubbers. In the prediction method described in the following the calculations are done iteratively with continual strain level corrections to the material moduli.Regarding material properties measurements, there could also be dependence on the laboratory, testing protocol, methodology and data analysis, as well as changes in rubber behaviour with age etc. that may result in variability in test results of the backing material. This issue was addressed in this study but published separately [10].
1.3 Measurement vs. Prediction
Direct testing, usually in the laboratory, has also been used to prove, compare and characterise indentation rolling resistance. Advantages are that results may include other loss sources associated with the belt deformation.Disadvantages arise with the difficulty in characterizing the wide range of application variables such as; loading, belt speed, temperature, idler diameter, belt construction, etc. – needed for use in conveyor design and the expense of building, maintaining and operating the test facility. Even direct measurement of the indentation resistance is subject to measurement error and assumptions. It may be noted that several of these test studies included comparison to predictions with the conclusion that indentation rolling resistance is not amenable to accurate predictive calculations. One of the intents of this paper is to address that suggestion.
2. Commonly used Indentation Rolling Resistance Models
Analytical and computational models of indentation rolling resistance of the belt backing by idler rolls have been developed and, for design purposes, the influence of the main parameters such as idler diameter, carry weight, backing thickness and rubber properties of the backing have been well identified with simple analytical approaches.Various analytical and computational models of the indentation rolling resistance calculation exist and are commonly used, from simple one-dimensional models of the steady rolling process, energy loss models, to full two-dimensional finite element calculations of the deformation and recovery process of the backing material moving over an idler roll. Indeed, the total loss for a particular idler is a three dimensional problem that must include loading variations across the width of the belt. This project is limited to uniform loading as shown in Fig. 2 so the third dimension is not addressed in this paper except through acknowledging the effect of incorporating the varying load across the idler roll.
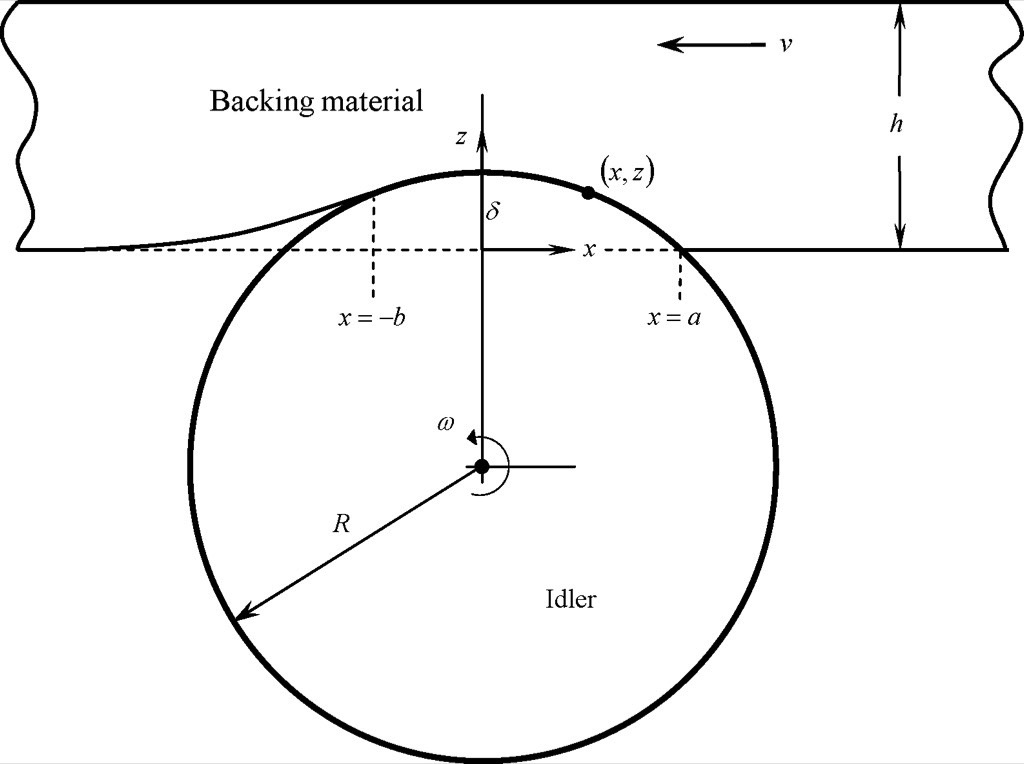
Prediction models are based on various assumptions and consequently may provide different results, even for the same material parameters. One aspect of modelling is that of the kinematics of the backing deformations. Another is how the indentation loss is derived from the deformation model.Jonkers [3] focuses on the energy dissipation rate of the cover material in a steady deformation cycle whereas Lodewijks [4] and others determine the power of the stress distribution at the idler/backing interface. In the latter case, the effective resistance force of the belt on an idler roll is related to this power through the moment of the interface stress distribution about the centre of the idler roll.As most models of indentation rolling resistance are viewed as a steady state process where the cover material moves though a “control volume” region around the idler roll interface, these two different approaches could also be characterized as energy dissipation and moment methods. Alternately, these are internal and external work perspectives.Differences result in these approaches, depending on the material model and the deformation modelling in each, but, of course, under the same assumptions, both the energy dissipation rate and the power methods must provide the same result, assuming no slipping at the idler/backing interface, by the conservation of energy principle.More complete deformation models such as those of May, et.al., [5] or Hunter [6], treat the backing as fully two-dimensional so that shear deformation occurs in the backing. These more rigorous models generally fall into the category of power methods and ensue from different material and deformation assumptions, and provide some differences in predicted resistance values. Lodewijks [4] has shown that indentation resistance values from these two dimensional approaches are somewhat higher than the one-dimensional models, but not by significant amounts for similar material models.One can also take a completely computational approach to this rolling contact problem, where the cover deforms as a two-dimensional medium and modelled by finite elements [8]. Like the power method mentioned above, the interface stress distribution and centre of reaction offset from the idler roller centre is iteratively determined to provide a resistive force on the belt.The advantage of a computational approach is that less restrictive deformation models are possible, such as modelling the entire belt carcass as may be important for cable reinforced belts where the deformation between the steel cables also dissipate energy. On the other hand, recourse to computational methods at the outset does not bring out important parameter dependence or may be time consuming and expensive for parameter studies.
2.1 One Dimensional "Winker Foundation" Models
Modelling of the cover layer as a Winkler Foundation provides a simple yet direct way to analyse the rubber deformation. Though rubber is known to deform in shear, the Winkler model assumes the belt cover to be a bed of independent longitudinal springs so that their deflection versus time can be modelled to conform to an indentation magnitude, see Fig. 3.
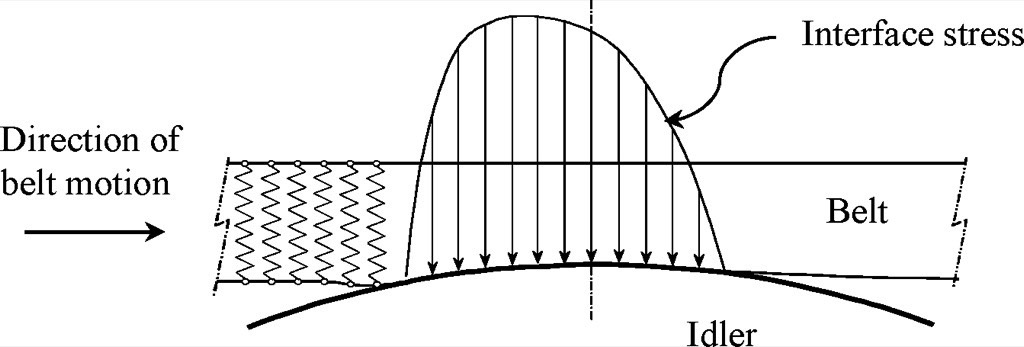
In the approach of Jonkers [3], the strain energy absorbed by the backing material is approximately determined. Rather than the actual stress/strain path, the load cycle is taken to be that of an elliptical path of the Lissajou oval.The methodology assumes that the deformation cycle experienced by the conveyor belt backing, modelled as a one-dimensional Winker foundation, is continually one of compression followed immediately by tension in a periodic, single frequency, sinusoidal cycle with a half wavelength equal to the contact length with the idler. The load balance – stress equilibrium equation and stress/strain determine the maximum strain, used to arrive at a "correction" for the rubber properties. This is described in Rudolphi and Reicks [10] and is used in the results presented in the following sections.Lodewijks [4] methodology is also used in the comparisons provided below. In this calculation, a formula for the contact stress, relating the carry load, contact length (and hence strains through the circular arc of the idler) and material viscoelastic parameters, is solved in an iterative process to determine the actual length of contact for the applied load.When the correct contact length is established, the stress and strain profile including the viscoelastic recovery under the idler roll is determined. Integration of the moment of the contact stress profile, about the idler center, then provides the moment of the rolling resistance force, and hence the equivalent rolling resistance force. The expansion of this method is provided by Rudolphi and Reicks [7] and is used in the results that follow below.
3. Direct Indentation Rolling Resistance Measurements
Direct measurement of belt cover indentation rolling is practically limited to a small set of operating conditions compared to the wide range of loads on a belt conveyor or the operating environment for a particular application, to say nothing about the combinations of belt and idler roll properties at the design stage. Nonetheless, direct measurements serve a very useful function comparing reality to predicted values from models which include various assumptions and extrapolations.Field measurements have practical challenges of separating the belt cover contribution from other losses as well as the difficulty in changing design variables. In addition, the roll load distribution is effectively integrated across the belt width in such measurements. Separating load from resistance makes it even more difficult to extrapolate for use in similar designs. Therefore, short laboratory tests with controlled parameters have been used as a measure of the accuracy of the various predictions discussed above.Recognizing that indentation rolling resistance is only important in the aggregate of many individual idler rolls underlines an additional major difficulty of sensitivity even when attempting to measure indentation loss in a controlled setting. That said, two direct measurements of indentation rolling resistance on the same belt cover rubber were performed to assess suitability of the selected prediction models. These are discussed briefly here with results provided below.
3.1 Overland Conveyor – Incline Roller Test
A test was developed which measures the acceleration of a rolling cylinder down an inclined plane. The difference in acceleration between the roller operating on the belt cover and on a rigid base is used as a measure of the loss due to the roller indentation into the rubber. Six inch diameter steel and steel covered nylon rolls provides two loadings.A sheet of the rubber to be tested is glued to a thin metal sheet, which is laid on a rigid, flat and inclined base. A 360 pulse encoder is attached to the centre of the roll and rotationally supported by a 36 inch (approx. 914 millimetre) torque arm, which is supported at its end with a 72 inch (approx. 1828 millimetre) string so that negligible rotation or resistance occurs during the 8 inch (approx. 203 millimetre) roller movement.The time is measured accurately between each rising step of the encoder and differences in time intervals can be used to calculate the changing velocity, or acceleration. Rather than measure the slope of the rubber cover accurately (within 0.006 angular degrees for 0.0001 friction discretion), a thin piece of steel is laid on the rubber, which prevents most indentation while conforming to the rubber macro surface. Results from these tests are provided in Section 4.
3.2 The Tunra – Recirculating Belt Test Facility
Tests measuring the rolling resistance of a short belt sample of the same belt cover material were made at the Tunra Bulk Solids laboratory at The University of Newcastle. The test setup is illustrated in Fig. 4. The test facility accepts pre-spliced endless belts up to 600 millimetres wide and 5500 millimetres long. The belt speed, idler roll diameter and vertical load can be varied and the influence of each parameter measured independently.
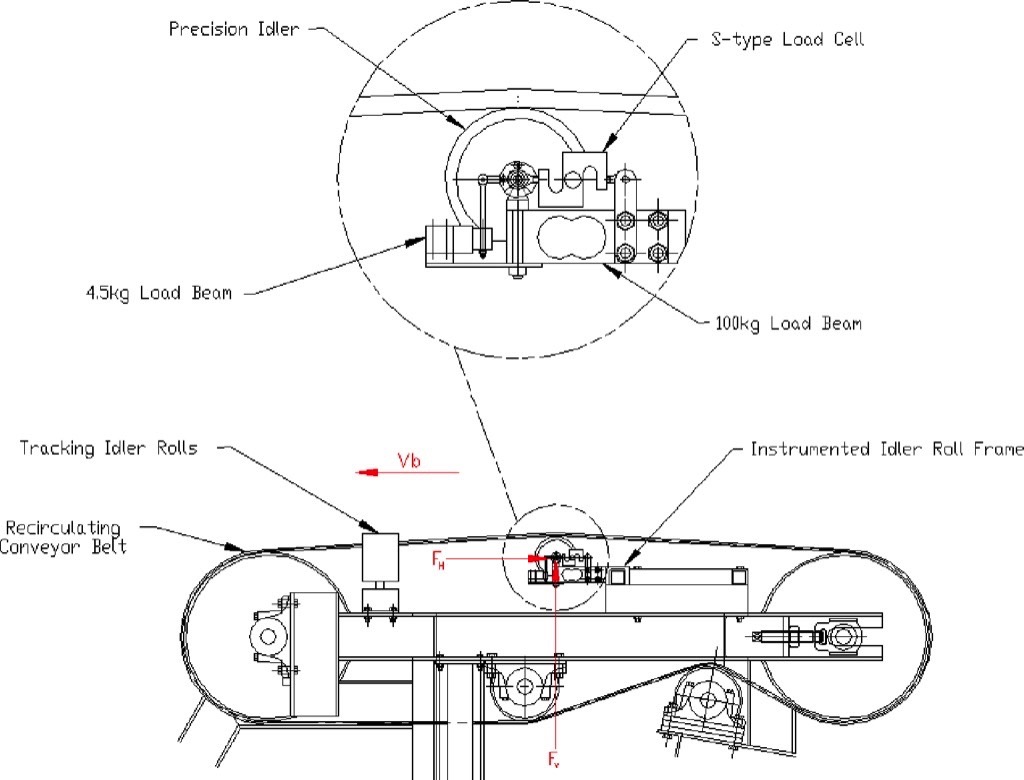
The applied vertical load is a result of the vertical component of the belt tension in addition to a minor component due to the self-weight of the belt. The vertical load is varied by adjusting the counterweight. To ensure the contribution of the belt flexural resistance is minimized the deflection of the belt over the instrumented idler roll is limited to conventional sag ratios, with 2.0 percent selected for this study.The total horizontal force Fh, acting on the idler roll is due to the indentation rolling resistance and the rotating resistance of the idler roll. Measurement of the horizontal force is undertaken using an instrumented idler roll that also measures the idler rotating resistance as a separate component. This enables the indentation rolling resistance to be isolated. The instrumented idler roll consist of a precision made shell which is machined both internally and externally to ensure concentricity and dynamic balance. The idler roll is supported at each end by a collar that is attached to the shaft.Each collar is supported on a knife-edge and rocker support that enables the vertical force to be measured by a 100 kilogram capacity load beam, while the horizontal force is measured by a 5.0 kilogram s-type load cell. The rocker support facilitates measurement of the vertical force, Fv while allowing horizontal movement which is restricted only by the s-type load cell. The knife-edge support allows the idler shaft to rotate freely about the knife-edge but is restricted by the 2.3 kilogram (5 pound) capacity load beam that measures the torque resulting from the rotating resistance of the idler roll.
4. Comparison of Predicted and Measured Indentation Loss
Since the purpose of the study presented in this article was to understand the error and accuracy of predictions, results of the various methods discussed above were compared to measured values at identical or at least comparable conditions, over a range of normal loads and the same rubber compound and viscoelastic measurements.The actual belt specimen tested was a solid woven carcass belt with both covers of the same rubber and thicknesses of 6 millimetre, while a 150 millimetre diameter idler roll was selected. Measurements of the indentation rolling resistance force were taken on the two test facilities described in Section 3. Measurements on the recirculating belt test facility were made at belt speeds of 1.0 to 5.0 metres per second, at loads of about 500 to 2000 Newton per metre and at a temperature of approximately 25°C. Similarly, calculations of the indentation resistance were performed by the methods of Section 2 over the same range of belt speeds and loads, at the test temperature, idler diameter and material properties from the same rubber cover compound.Results of the recirculating belt test facility are shown labelled as "Tunra" in Fig. 5, together with calculations made by the two methods described in Section 2. All calculation methods assume a temperature of 25°C and include that of Jonkers [3] (labelled "M1") and the generalized method of Lodewijks [4] (labelled "M2").
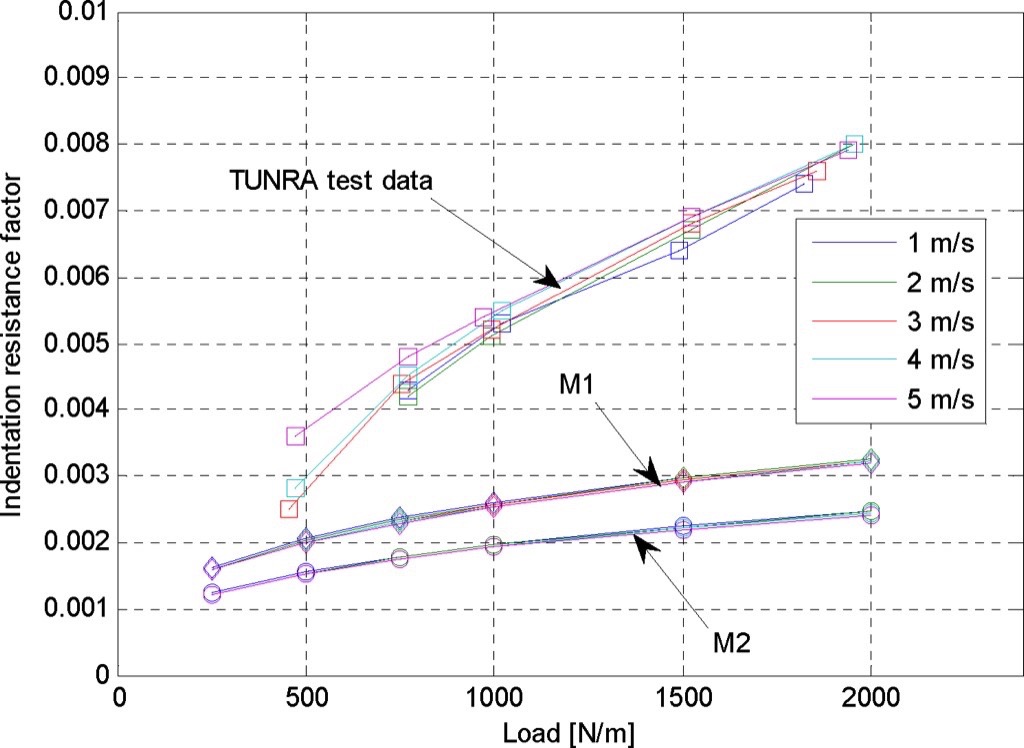
All calculations shown in Fig. 5 are based on viscoelastic data taken at low strain. Also, in the calculation method of Jonkers, modulus E' was determined from the master curve at a frequency of π·v/(a+b), where v is the belt speed and (a+b) is the idler/ cover contact length, which was established through the iterative process of Lodewijks’ method.Several observations are immediately clear from Fig. 5.
- Within the range of tested belt speeds, the measured and calculated values of the indentation resistance are nearly independent of the belt speed. This is especially true from the calculated values and fairly well corroborated in the measured values.
- The calculated values are all considerably less than the measured data and have less load dependency. These represent methods that have been used for conveyor design in the past.
- The energy dissipation method of Jonkers is somewhat higher than the stress power or moment methods of Lodewijks as expected. (Lodewijks [4]). This is due to the presumption of initial tensile strain inherent to the method.
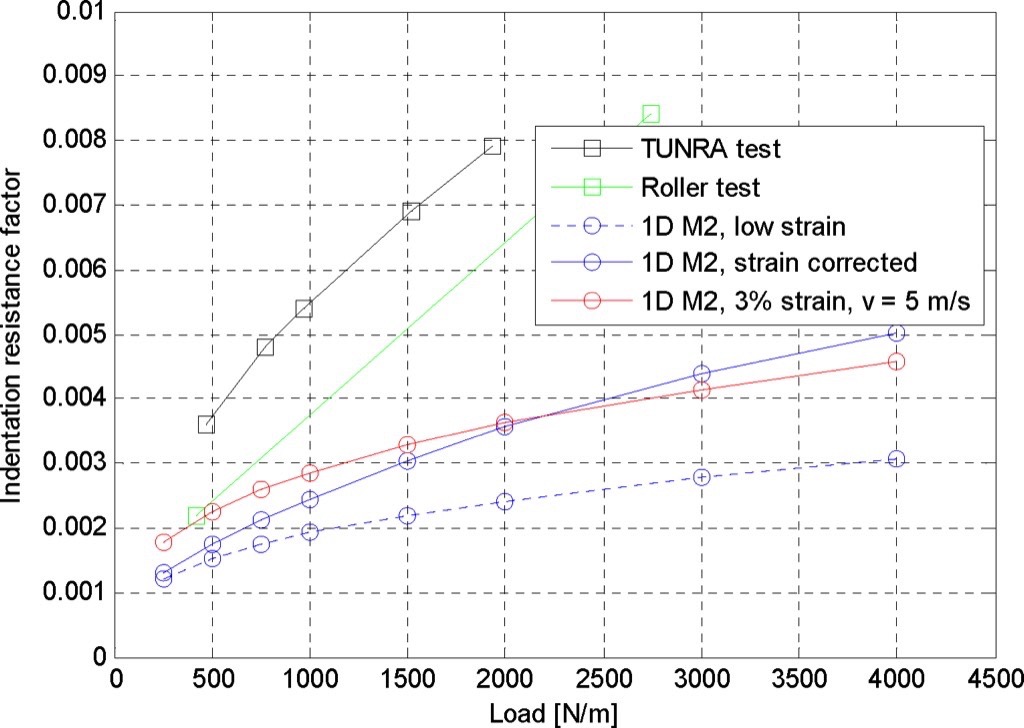
Based on observation (a) that the indentation resistance is nearly belt speed independent for this cover compound, further comparisons were performed at the single belt speed of 5.0 metre per second.Fig. 6 shows the effect of using the strain amplitude corrected material properties as outlined in Section 2, for the Jonkers’ method, "M1", and the Rudolphi Reicks adaptation of Lodewijks’ method, "M2". Those calculated values, along with the measured values of both tests and the non-strain corrected calculated values, are shown in Fig. 6. Note measurements were made at two loads only for the incline roller tests.
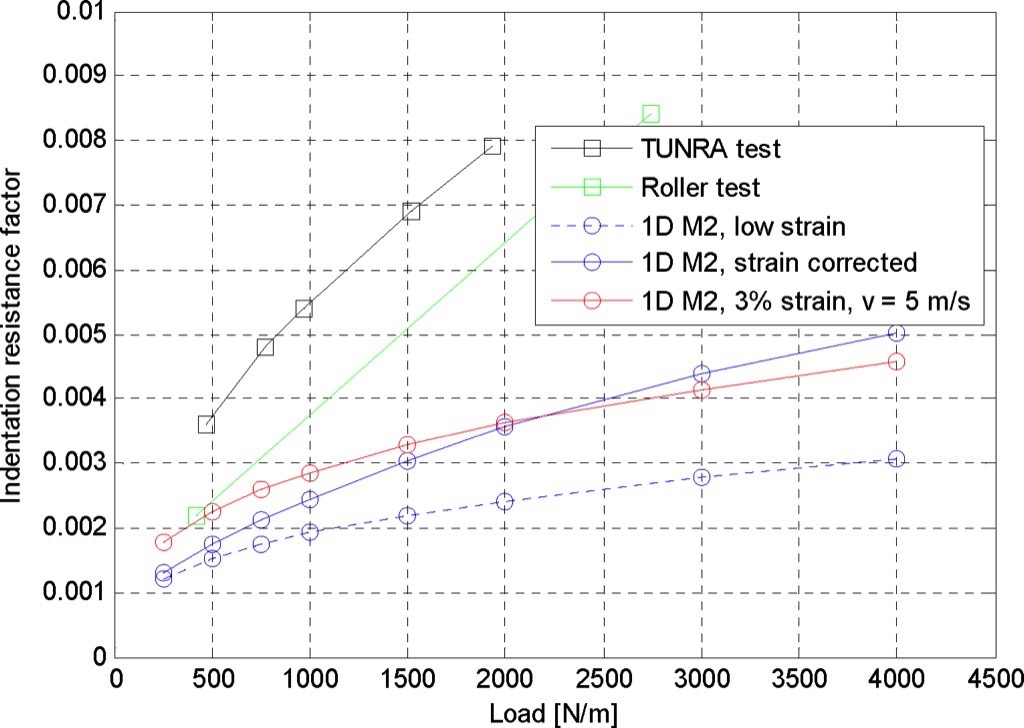
From the results presented in Fig. 6 we further observe that:
- Low strain and strain corrected prediction results are similar at low load where the strain is low.
- The strain corrected calculations are higher than those based on non-strain corrected rubber properties and diverge more steeply as the strain effect increases with increasing loads.
- The 3 percent strain test data provides parallel but higher loss prediction than those from the low strain data and crosses the strain corrected data at a load representing 3 percent strain in the backing material.
- The two measured values with the Inclined Roller test correlate fairly well with the measured values from the Tunra test facility, but both sets of experimental data are higher than predicted.
- Even though the strain corrected calculations trend better to the measured values than the non-strain corrected (‘low strain’) results, they are still considerably lower than the measured values.
Point (c) illustrates that use of rubber test data at high strain provides higher loss predictions which better match test results at intermediate loads but are too high at low loads. Points (d) and (e) lead to the question if indentation rolling resistance may not be the only loss taking place during the testing. In both cases, care was taken to ensure adhesion between the test roll and the rubber was not an important contribution by using talc or a weathered surface as would occur in normal operation. Both had continuous substrates with expected low potential for added deformation at the interface.In reviewing the Tunra tests, additional rubber deformation due to a constant 4.6 degree bend angle (equivalent to a belt deflection to idler roll spacing ratio of 2 percent) is applied by the instrumented idler roll to provide the indentation load. This bending causes a fully reversed strain cycle on both sides of the belt carcass, normal to the indentation. The magnitude of this viscoelastic loss was approximated, assuming a full cycle of the bending strain of both covers, and the hysteretic loss (area within the elliptic, Lissajous stress/strain cycle), similar to Jonkers’ method for indentation. This effective loss value was then subtracted from the Tunra test result and corresponds to the "corrected" curve as shown in Fig. 7.
The details of this correction are provided as an appendix in this PDF available for download here: bsh2012_03_07_Reicks_Appendix.The bending corrected results of Fig. 7 provide good correlation between predicted and measured results, especially at low load. Note the reduction in measured loss credited to indentation as well as the change in trend with load. The latter is due to the small change in bending radius with belt tension and therefore roll load. They also identify the potential importance of belt bending loss as another loss mechanism.Nonetheless, the divergent slope of test versus prediction suggests another load dependent loss or correction is not addressed. Variation of strain through the cover thickness may be one of these.
5. Summary of Work and Discussion of Results
This article reviews the use of several methods for predicting the energy lost during repeated indentation while the conveyor belt cover runs on idler rolls. It was established that modelling rubber deformation in one dimension with the "Winkler foundation" model provides reasonably accurate results.With the bending correction applied, the comparison of quantifying a strain cycle made by cyclic laboratory tests or by indentation seems to be tolerant of the actual modelling mechanism. That is, indentation loss can be predicted with reasonable accuracy.It was also found that the range of strains common in conveyor belt covers cause significant changes in the rubber behaviour, requiring some method of incorporating this form of non-linearity when determining stiffness and loss values. The strain corrected approach adopted in the current work uses a non-linear material model in conjunction with a one-dimensional deformation model, based on the assumption that every point in the backing undergoes the same strain amplitude.Several other assumptions made in the prediction models that can affect the accuracy of the predictions should be acknowledged. These include:
- The rubber deformation is assumed to be zero at a fixed boundary at the bottom of the belt cover. A solid woven carcass was specified for the test belt to match this condition but other research [9] has shown that steel cable carcasses, for example, have additional losses due to the additional rubber deformation between the cords so that this assumption may not hold for all applications.
- The rubber stays attached to the idler roll at a point of initial contact so that no frictional sliding occurs.
- Rubber theory also includes an adhesion mechanism that retards the roller at the trailing point of contact separation. This was seen with clean fresh test rubbers in the roller test but is eliminated with the application of talc. It seems reasonable that this same phenomenon occurs when operating in most bulk handling environments.
- While not accounted for in the usual conveyor energy loss calculations, belt bending was found to be an additional and potentially significant source of loss that is not usually considered when calculating rubber viscoelastic loss.
It should be clear that a useful application of this prediction requires a proper integration to the load profile across conveyor idler rolls and an understanding of several other sources of loss, perhaps including belt bending. It should be understood that the bending discussed in Appendix A applies only to the test case used for the measurements in this project. Actual belt bending loss is due to the real belt sag of the troughed belt from the distributed material loading and also varies across the belt width.
Conclusion
This paper confirms that a design relevant indentation loss prediction can be calculated by applying a sufficiently detailed and accurate material model if it includes nonlinear strain effects of the belt cover rubber.
A Note from the Editor
For all statements in this article that refer – directly or indirectly – to the time of publication (for example “new”, “now”, “present”, but also expressions such as “patent pending”), please keep in mind that this article was originally published in 2012.
References:
- Ferry, J.D.: Viscoelastic properties of polymers. 3rd Edition, Wiley, New York 1980.
- Rudolphi, T.J.: Applied rubber belt cover loss prediction from indentation. 2008 SME Annual Meeting and Exhibit, Salt Lake City, UT, Feb. 24-27, 2008.
- Jonkers, C.O.: The indentation rolling resistance of belt conveyors – A theoretical approach. Fördern und Heben, Vol. 30 (1980) No. 4, pp. 312-317.
- Lodewijks, G.: The rolling resistance of conveyor belts. bulk solids handling, Vol. 15 (1995) No. 1, pp. 15-22.
- May, W.D., Morris, E.L., and Atack, D.: Rolling friction of a hard cylinder over a viscoelastic material. Journal of Applied Physics, Vol. 30 (1959) Vol. 11, pp. 1713-1724.
- Hunter, S.C.: The rolling contact of a rigid cylinder with a viscoelastic half space. Journal of Applied Mechanics, Vol. 28 (1961), pp. 611-617.
- Rudolphi, T.J., and Reicks, A.V.: Viscoelastic indentation and resistance to motion of conveyor belts using a generalized Maxwell model of the backing material. J. Rubber Chemistry and Technology, June (2006).
- Wheeler, C.A.: Analysis of the main resistances of belt conveyors. Ph. D. Thesis, The University of Newcastle, Australia, (2003).
- Wheeler, C.A., and Munzenberger, P.J.: Predicting the influence of conveyor belt carcass properties on indentation rolling resistance. Bulk Solids and Powder: Science and Technology, Vol. 4 (2009). pp. 67-74.
- Rudolphi, T.J., and Reicks, A.V.: The importance of nonlinear strain considerations in belt cover indentation loss. bulk solids handling, Vol. 32 (2012) No. 2, pp. 52-57.
| About the Authors | |
| Allen V. Reicks, P. E.Director Research & DevelopmentOverland Conveyor Company, USA | |
| Prof. Thomas J. RudolphiDepartment of Aerospace EngineeringIowa State University, USA | |
| Prof. Craig A. WheelerAssociate Director of TUNRA Bulk SolidsUniversity of Newcastle, Australia |
■







