(From the archive of ”bulk solids handling", article published in Vol. 34 (2014) No. 4 , ©2014 bulk-online.com)
Introduction
Transfer stations between belt conveyors and other mechanical transport units are widely used in industry. They are particularly important for large mass flow rates as it is often the case in the mining industry, ports, or power plants. If dry material is conveyed the resulting dust emission can become a critical problem due to the increasing environmental and occupational health and safety regulations. Transfer stations are a main source for dust emissions in such plants. Hence, different methods are used to reduce the dust emissions. The majority of these methods can be called “active” dust suppression methods because they use additional energy or resources like water.In particular, the use of water sprinklers or sprayers has many disadvantages because increasing the moisture content may negatively influence the flow behaviour of the material and decrease the caloric value (e.g. in terms of coal). Also, in many geographical locations the amount of water needed for dust suppression does not exist or the temperatures do not allow the use of liquid water. Another “active” measure is the use of electrical energy (exhaustion fans), however many filters of such plants need water for regular cleaning. Dry filter cleaning systems often have less performance and may increase the dust emission during the cleaning operation. However, water based filter cleaning systems have the same problem like sprinkler or spraying systems: they need a large amount of water in liquid form.Due to the problems associated with active dust suppression systems, more and more “passive” systems are becoming important. The aim of such passive systems is to prevent the separation of dust from the main material stream. Due to the fact that dust is usually generated where wind is blowing across the bulk surface or where the porosity of the material stream changes abruptly, belt covers and transfer stations are the most important passive dust suppression systems.This paper focuses on the question of how a transfer station must be designed to keep the dust inside the material stream and hence minimise dust emissions. To predict the dust emission of a transfer station it is usually not enough to analyse the material flow but also the air flow inside the station. Computer simulations based on the Discrete Element Method (DEM) for the bulk material flow and / or computer simulation based on Computational Fluid Dynamic (CFD) for the gas flow are the most common ways to analyse the dust emission problem due to the varying and sophisticated design of many transfer stations and the complex nature of the air flow.
1. General Simulation Approaches
There is a variety of simulation approaches that can be used to analyse the bulk material and gas stream inside transfer stations. One method is to use a two phase Euler-Euler approach to model a dense material stream in CFD [1]. This method uses CFD alone as the analysis tool; however there are certain limitations associated with this approach due to the fact that the bulk material is modelled as a fluid. This approach is applicable to predict the bulk material flow in thin layers of homogenous material with a rather fine particle size distribution. The second approach combines DEM and CFD simulation and has been used to analyse a transfer station with a very basic design consisting only of an incoming and outgoing conveyor belt. DEM analysis is used to predict the shape and the porosity distribution in the bulk material stream, with these parameters then used in an initial CFD simulation which calculates the air flow inside the material stream. In a second CFD simulation the air flow around the bulk material is calculated. This approach considers that the air flow is initiated and influenced by the material flow but the particle behaviour inside the material flow is not influenced by the air flow. The approach and its use for the prediction of dust emissions is described in more detail in [2]. The biggest disadvantage of this approach is obviously the increased complexity associated with its application to complex material flows as they arise from the use of impact plates, rock boxes and chutes.The third and most general approach, highlighted in this paper, is the direct coupling of DEM and CFD simulations. The interaction of bulk material and the surrounding air is important in many fields of bulk material handling and process engineering (e.g. pneumatic conveying, fluidised bed technology, etc). Hence, a lot of work has already been done in the field of coupling DEM and CFD [3-7]. A direct (simultaneous) coupling of DEM and CFD is especially necessary if the particles - fluid/gas interaction influences the particle velocity which is usually the case for high fluid/gas velocities or small particles. Simultaneous coupled DEM-CFD simulations show an even higher numerical effort than DEM or CFD simulation itself. However, nowadays the open-source DEM software LIGGGHTS [8] together with the open source CFD-DEM coupling framework CFDEMcoupling [9] enables the fast simulation of such problems due to use of sophisticated highly parallel DEM and CFD algorithms.Hence, this approach of directly coupled DEM-CFD simulations should be applied for the dust prediction in transfer chutes. The results from this new approach will be compared to someof the CFD-only simulations and experimental results presented in [1].
2. Preliminary Investigations
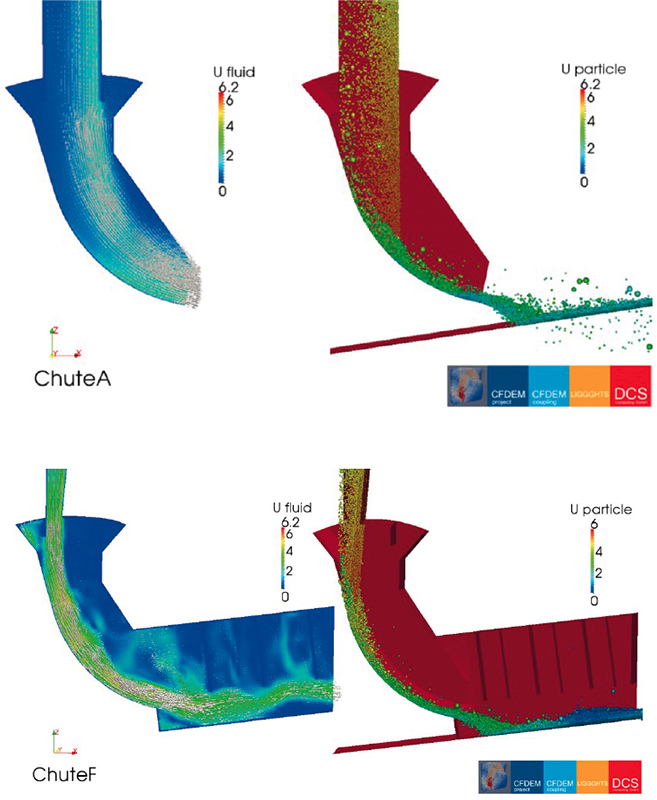
To minimise the dust emission of a specific transfer station the original design and five optimised design versions were tested experimentally and in computer simulations by the Centre of Bulk Solids and Particle Technology (CBSPT) at The University of Newcastle (Australia). All results of the investigations are described in more detail in [1]. In the following section only those details will be explained which are necessary for the understanding of the new directly coupled DEM-CFD simulations.From the six transfer chute designs in [1], the original (A) and the final design (F) were simulated within this paper (see Fig. 1). Chute F shows several additions like a restrictor plate, a stilling chamber and a closed lower opening in comparison to chute A.
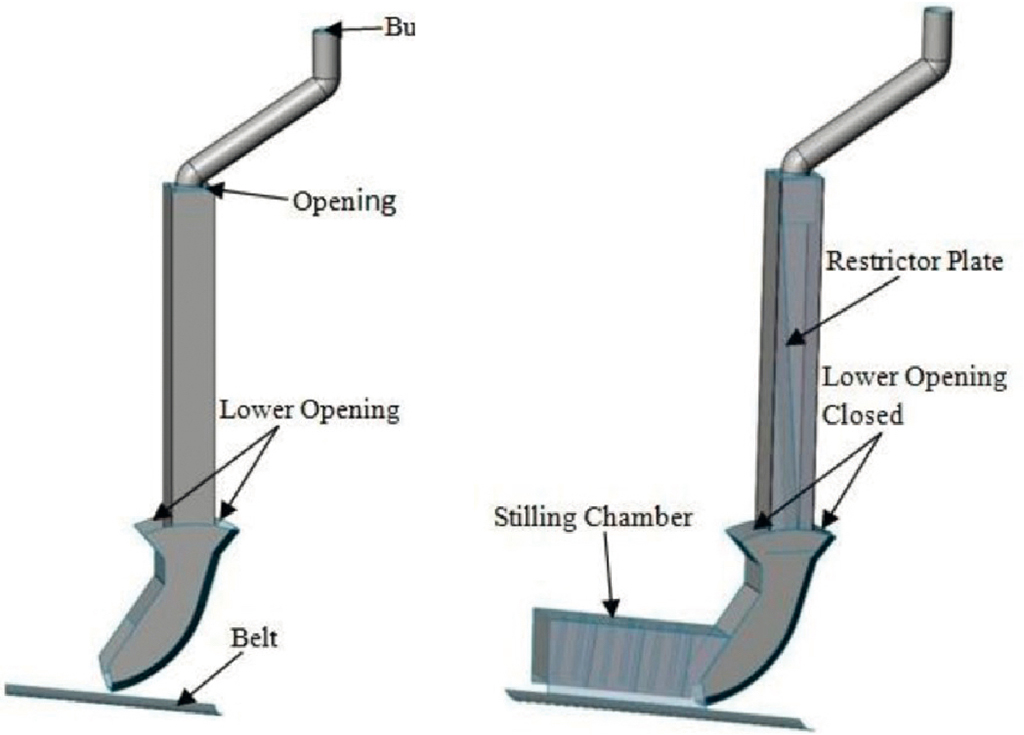
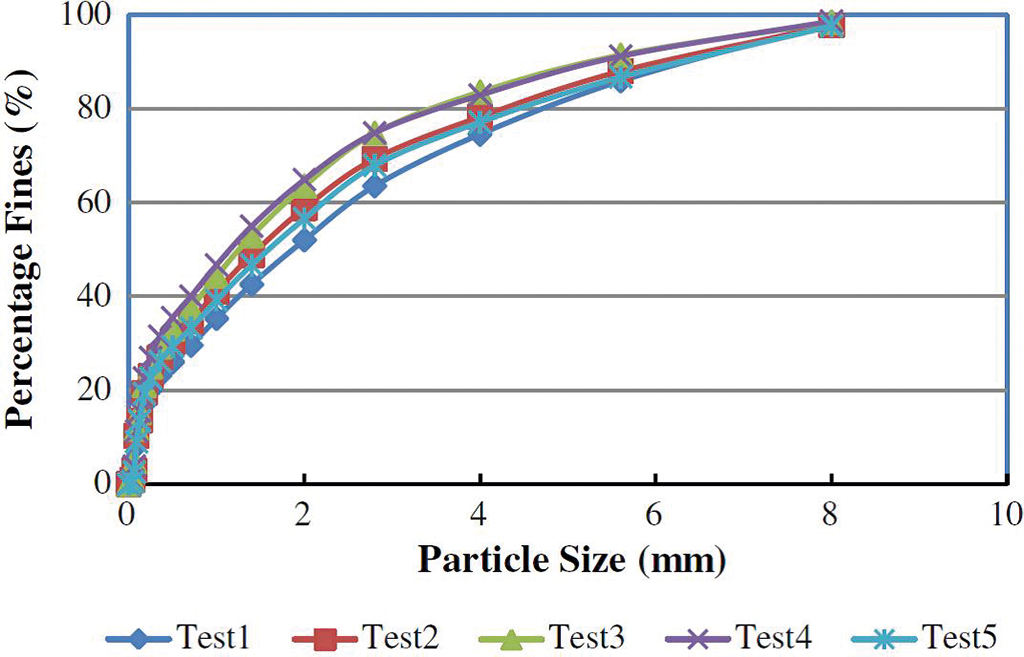
For the experimental tests a laboratory-scaled transfer chute was built at the CBSPT. Iron ore with the particle size distribution shown in Fig. 2 was used for the tests.
The chute was installed in an enclosure with the dimensions of 2.5 m wide, 2.5 m long and 3.0 m high. To capture the dust expelled from each transfer chute during testing, sheets of plastic were laid out over the floor of the enclosure. Due to symmetry of the enclosure and each chute the plastic sheets were placed only on one side of the enclosure. To enable the relative position of dust deposition to be determined, the enclosure was divided into four collection zones. The plastic sheets were left in the enclosure for the duration of each test and remained in place for 15 minutes after to allow settling of suspended dust before removal and weighing. All dust collected on the plastic sheets, as well as the dust that settled on the uncovered side of the enclosure was returned to the bulk material sample after each test. The main result of the extensive experimental program that is extracted for the purposes of this paper is that chute F showed a reduction of 75% of the total average dust emission in comparison to the transfer chute A (original design).
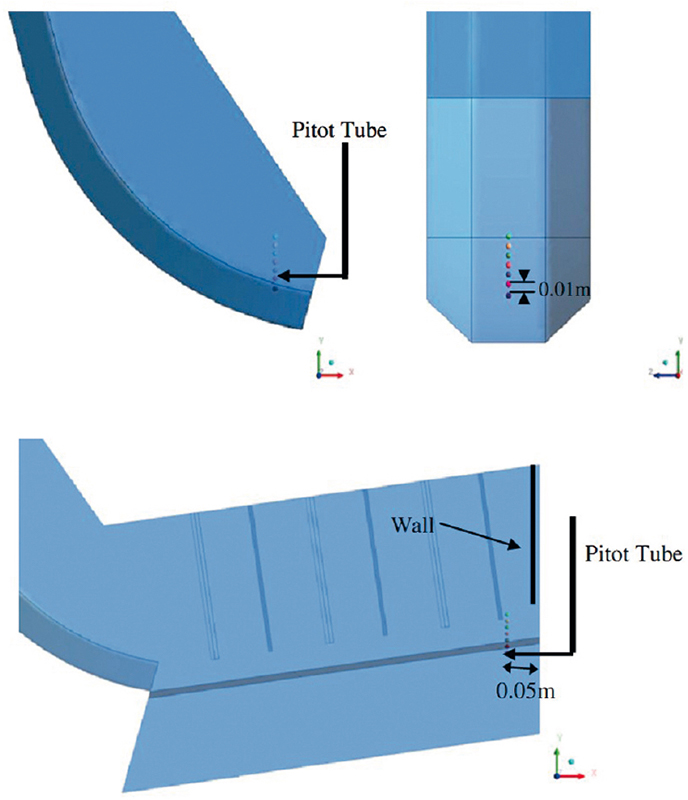
Additional to the measurement of the dust deposition on the plastic sheets, the air velocity was measured in the experiments to compare real measurement data with the results from the CFD simulations. Fig. 3 shows the position of the measurement points for the two types of chutes. A comparison of the air velocity results will be shown later in section 3.2.Within previous work [1], the commercial CFD software FLUENT was used to analyse air and particle flow in the chute enclosure to predict the likely performance of each transfer chute configuration with respect to dust emission. The relative performance of each design was predicted by analysing the air velocity and air mass flow rates.Due to the high volume fraction of particles, a two-phase Euler–Euler approach was adopted to model the granular stream and air flow in the transfer chutes. A Eulerian treatment was used for both the fluid and solid phase. A single pressure is shared by the air and particles, and the continuity and momentum equations solved separately for each phase.The air was assumed to be incompressible and at a constant density, while the particles were assumed to be spherical and have a uniform density. A particle diameter of 4 mm was selected for the simulations. The particle diameter was selected to limit the average computational time for each chute configuration to less than 10 days, in addition with reference to the PSD results shown in Fig. 2 , where more than 75% of the bulk material was less than 4 mm. The stress tensor of the solid phase is based on the continuum model of dense-gas kinetic theory of Gidaspow and Bezburuah [10] and considers the inter-particle friction force at high solid packing ratios. The fractional viscosity is included in the calculation using the friction model of Schaeffer [11]. The coefficient of restitution between particles was assumed to be 0.9.The results of the CFD simulations with the two phase Euler-Euler approach are shown in Fig. 4. The analysis of the air velocity will be discussed in Section 3.2.
3. Directly Coupled DEM-CFD Simulations
3.1 Model Description
The method presented here resolves the fluid and particle calculations by two strictly separated codes. The interaction is realised by exchange fields being evaluated in a predefined time interval, where the codes work in a sequential manner. Both the CFD and the DEM code do their calculations in parallel using Message Passing Interface (MPI) parallelisation. Also data exchange between the codes is realised using MPI functionality.This comprehensive model for three phase flow (fluid, dust and particles) is realised in a modular approach, where distinct physical phenomena are treated by dedicated sub-models. In this section the governing equations of all subroutines of this model approach will be highlighted.
3.2 DEM Method
The Discrete Element Method was introduced by Cundall and Strack (1979) [12]. A very brief description of the method will be provided in this section. Further details on the contact physics and implementation issues are available in the literature (e.g. Zhu et al., 2007 [13]).The strength of the DEM lies in its ability to resolve the granular medium at the particle scale, thus allowing for realistic contact force chains and giving rise to phenomena induced by particle geometry combined with relative particle motion, such as particle segregation by percolation. Thereby, the DEM is able to capture many different physical phenomena, such as dense and dilute particulate regimes, rapid- as well as slow granular flow and equilibrium states or wave propagation within the granular material.Thanks to advancing computational power, the DEM has become more and more accessible lately. On actual desktop computers, simulations of up to a million particles can be performed. On very large clusters, the trajectories of hundreds of millions of particles can be computed (e.g. LAMMPS, 2011 [14]).
-
Governing Equations
In the framework of the DEM, all particles in the computational domain are tracked in a Lagrangian way, explicitly solving each particle’s trajectory, based on the force and torque balances:
and
 |
where Fp,n is the normal contact force, Fp,t is the tangential contact force. Fp,f is the drag force exerted from the fluid phase to the particles, Fp,p and Fp,v denote respectively the pressure and viscous force acting on the particles. Other body forces like gravity, electrostatic or magnetic forces are lumped into Fp,b. For sake of completeness, these forces are described in detail in Table 1.
| Forces | Correlations |
| Fp,n | |
| Fp,t | 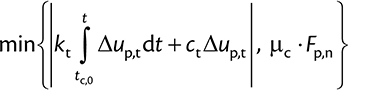 |
| Fp,b | |
| Tp,r | |
| ωrel | |
| Fp,p | 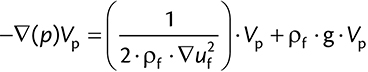 |
| Fp,v | |
| Fp,f | |
| *Drag force FD is explained in Goniva at al. (2012) [15] | |
Each physical particle is mathematically represented by a sphere, another geometrically well-defined volume or a combination of them. The translational and angular accelerations of a sphere are based on the corresponding momentum balances. Generally, the particles are allowed to overlap slightly. The normal force tending to repulse the particles can then be deduced from this spatial overlap Δxp and the normal relative velocity at the contact point, Δup,n. The simplest example is a linear spring-dashpot model, shown in Fig. 5.
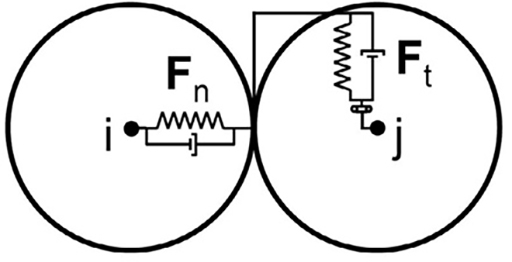
An efficient way of taking into account the small-scale non-sphericity of the particles is a rolling friction model, see Goniva et al. (2012) [15]. It introduces an additional torque also for collisions, where the relative velocity at the contact point is zero. Within this paper a directional constant torque model (Ai et al., 2011 [16]), is applied (see Table 1).
3.3 CFD-DEM Method
For the modelling of particle laden fluid flow a coupled CFD-DEM approach can be applied (Tsuji et al. [4]; Zhou et al. (2010) [17]).
-
Governing Equations
The motion of a fluid phase in the presence of a secondary particulate phase is governed by the volume-averaged Navier-Stokes Equations for compressible fluid, which can be written as:
 |
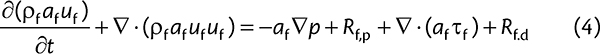 |
Here, af is the volume fraction occupied by the fluid, ρf is its density, uf is its velocity, and τf is the stress tensor for the fluid phase. Rf,pre presents the momentum exchange with the particulate phase, which is calculated for each cell, where it is assembled from the particle based drag forces. Rf,d represents the momentum exchange with the droplet phase. For solving the above equations a pressure based solver using “Pressure-Implicit Split-Operator” (PISO) pressure-velocity coupling is used, where an implicit momentum predictor followed by a series of pressure solutions and explicit velocity corrections is performed (Jasak, 1996 [18]).
-
CFD-DEM Coupling Routine
The coupling routine consists of several steps:
- The DEM solver calculates the particle positions and velocities.
- The particle positions, velocities, and other necessary data are passed to the CFD solver.
- For each particle, the corresponding cell in the CFD mesh is determined.
- For each cell, the particle volume fraction as well as a mean particle velocity is determined.
- Based on the particle volume fraction, the fluid forces acting on each particle are calculated.
- Particle-fluid momentum exchange terms are assembled from particle based forces by ensemble averaging over all particles in a CFD cell.
- The fluid forces acting on each particle are sent to the DEM solver and used within the next time step.
- The CFD solver calculates the fluid velocity taking into account local particle volume fraction and momentum exchange of the granular and droplet phase.
- Additional equations such as dust concentration are evaluated.
- The routine is repeated from (1).
-
Fluid-Particle Momentum Exchange
Once the particle volume fraction is calculated it is possible to evaluate each particle’s contribution to particle-fluid momentum exchange, which is mostly established by means of a drag force depending on the local particle volume fraction.For numerical reasons the momentum exchange term is split-up into an implicit and an explicit term using the cell-based ensemble averaged particle velocity ‹up›:
where
 |
For the calculation of Kf,p many different drag correlations have been proposed during the recent years (e.g. Zhu et al. (2007) [13]). Within this paper a drag relation based on lattice Boltzmann simulations proposed by Koch and Hill (2001) is used, see Goniva et al. (2012) [15].
-
Dust Propagation
For the dust phase a passive scalar transport equation is solved. It is assumed, that the dust loading is very low and thus an influence of the dust on the gas phase can be neglected. This assumption is perfectly suited for the dust sized considered in this investigation. The transport equation consists of a transient, convective, diffusive and source term and can be written as follows:
 |
where ∂T is the dust concentration, DT the dust diffusion and ST is a source term of the dust phase.As described by Goniva et. al. (2010) [21], dust diffusion is strongly affected by the local turbulence. Following Crowe (1985) [22] the reciprocal Schmidt-number, which is the ratio of diffusivity and effective viscosity, is a function of the ratio τP,relax/τG,turb,
 |
where τP,relax is the particle relaxation time and τG,turb the characteristic time scale of the fluid turbulence, which can be calculated from the turbulence parameters k und ε:
 |
If the dust particle diameter is in a size range where the settling velocity is not negligibly small, an additional drift velocity has to be introduced (see Goniva et al. 2010) [21]. For the dust particles considered here this can be neglected.Bagnold (1941) found that, dust emission from the surface of a granular bed is a function shear velocity at the surface and can be described by F·µ·u3. Within this investigation we assumed, following Hilton und Cleary (2011) [23], that a dust source can be modelled as follows:
 |
where C is a model parameter, Vcell the cell volume and rp the particle radius.
-
Coupled CFD-DEM Solver
The coupled CFD-DEM approach described above was implemented within an open source environment (Goniva et al. (2012) [15]; Kloss et al. (2012)[19]). The CFD part of the simulations as well as the Lagrangian droplet tracking is conducted by a solver realised within the open source framework of OpenFOAM® (OpenCFD Ltd., 2009 [20]). The coupling routines are collected in a library providing a modular framework for CFD-DEM coupling (CFDEMcoupling, 2012 [9]). The DEM part of the simulations is conducted in LIGGGHTS, an open source software package for modelling granular material by means of the discrete element method (LIGGGHTS, 2012 [8]) based on LAMMPS, an open source molecular dynamics code by Sandia National Laboratories for massively parallel computing on distributed memory machines.Both LIGGGHTS and CFDEMcoupling run in parallel using message-passing techniques (MPI) and a spatial-decomposition of the simulation domain. LIGGGHTS and CFDEMcoupling are distributed as open source codes under the terms of the GNU General Public License (GPL). A selection of coupling routines as well as example solvers are provided at a dedicated web page maintained by the authors (CFDEMcoupling, 2012 [9]).
3.4 Results
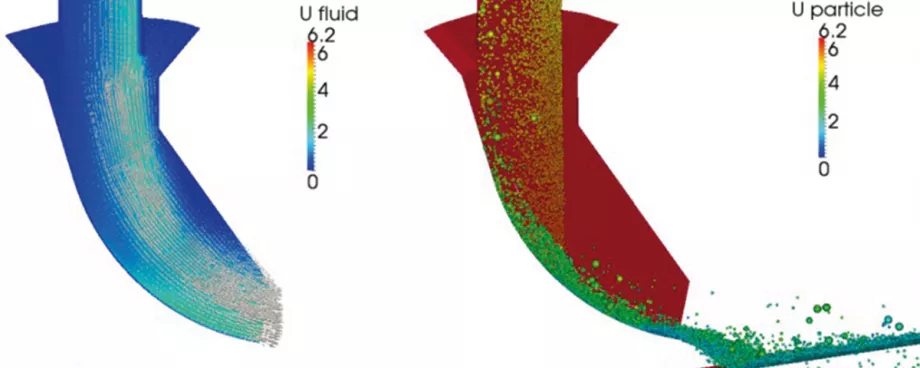
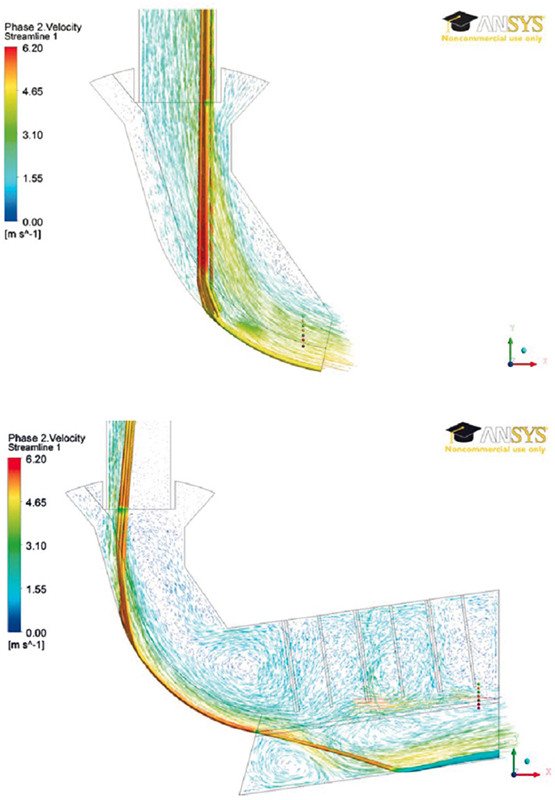
Applying the coupled CFD-DEM model approach highlighted in the previous sections, the air flow-rates as well as the dust generation of two different chute configurations (Fig. 1) are investigated. A qualitative result of the fluid and particle flow is pictured in Fig. 6. For both chute setups the gravity driven particle flow induces air flow which then transports the generated dust.
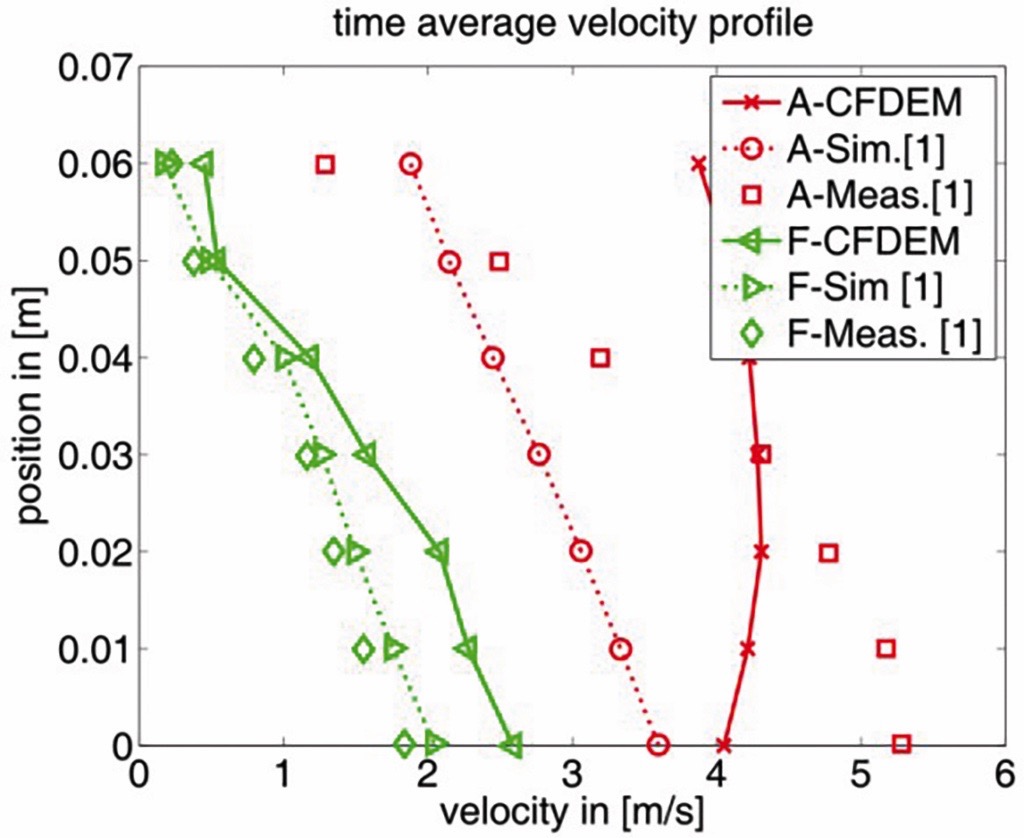
A quantitative comparison of the air velocities at the outlet of the chutes is given in Fig. 7. The obtained data for chute F is in very good accordance with measurements [1] as well as Eulerian multiphase simulations [1]. For Chute A the average air velocity matches the measurement data, but the flow profile deviates from the measured data.
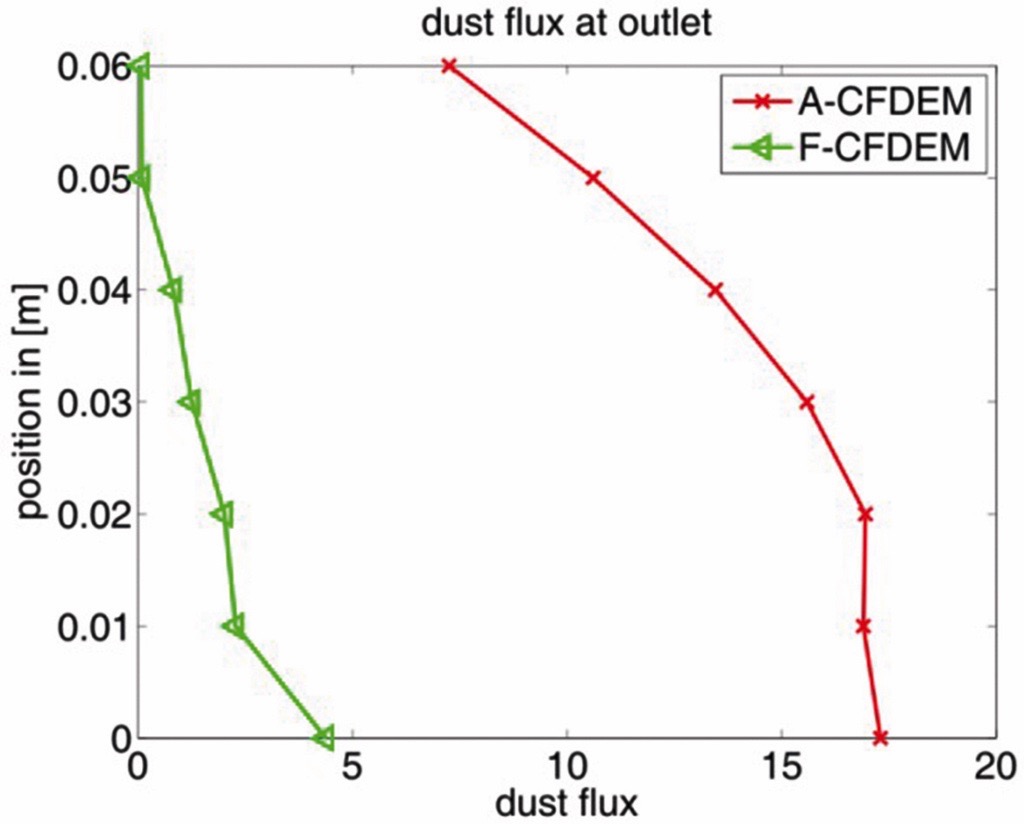
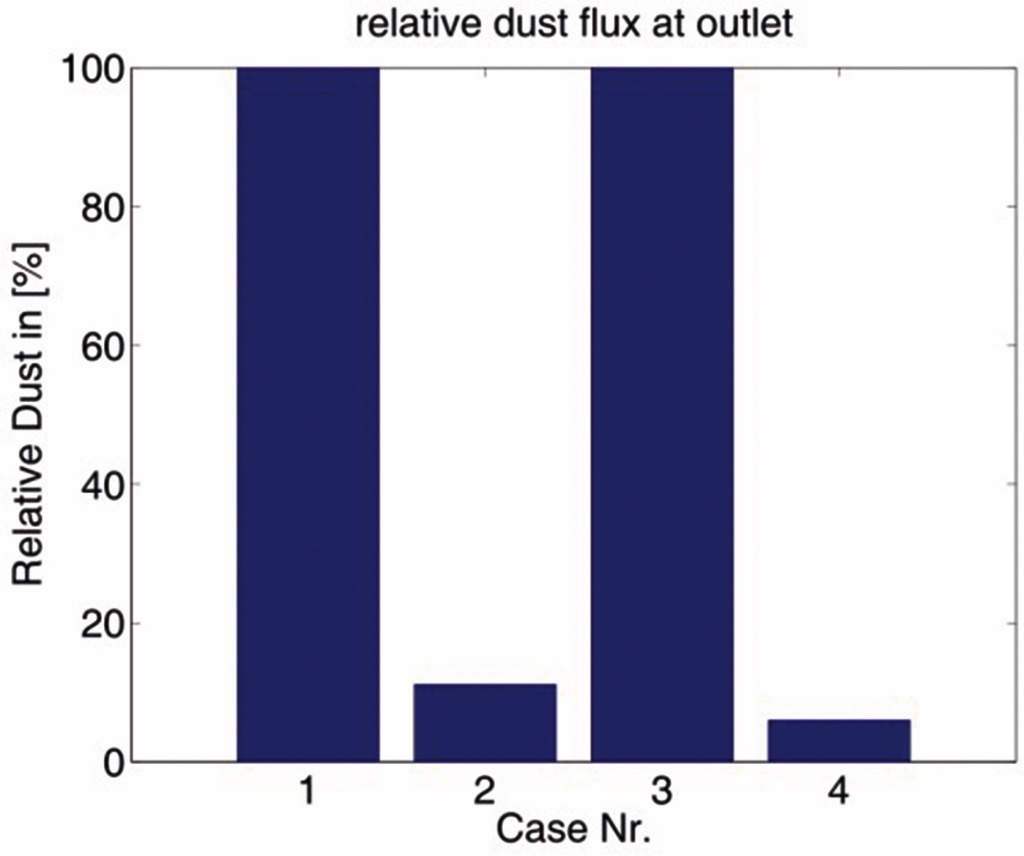
Applying the passive scalar transport equation for the dust phase transport (Eq. (7)) and generation (Eq. (10)) the dust flux can be calculated. According to earlier measurements [1] the dust flux for chute A is significantly higher than for chute F. Compared to chute A, the calculated dust flux of chute F is reduced by 88.9% (Fig. 9). Measurements [1] predicted even a dust reduction of 94%.
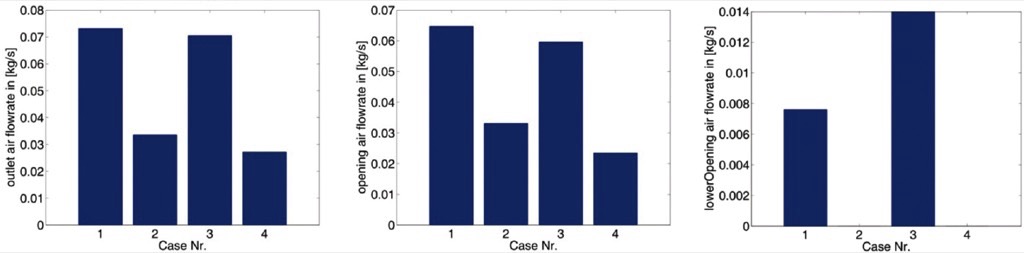
The induced air flow predicted by coupled CFD-DEM simulations is in good quantitative accordance to Eulerian multiphase simulations [1] (Fig. 10). Only for the lower opening, the results slightly differ.
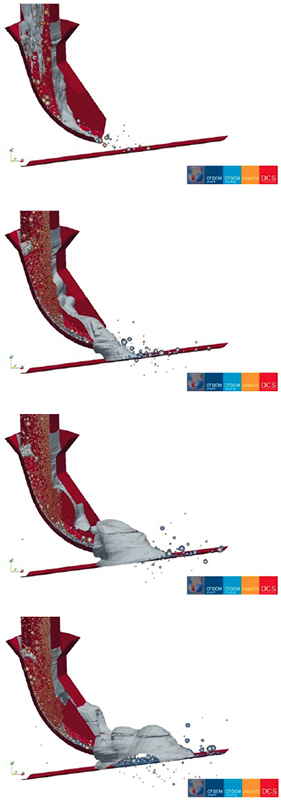
A visualization of the dust propagation at the outlet section of chute A is given in Fig. 11, where an iso-surface of dust concentration is tracked over time. Such a prediction of the dust propagation is perfectly fitted to detect “hot-spots” and optimize geometry and ventilation systems.
Conclusions
Within this paper a fully coupled CFD-DEM approach including a passive scalar transport equation for the production and propagation of fine dust is presented and applied to the particulate flow in two different transfer chute designs. The calculated data is compared to measurement data and Eulerian multiphase simulations, both published recently in literature [1]. The calculated induced air flow, which is the main driving force of the dust propagation, is in excellent accordance to existing measurement and simulation data [1].Compared to a Eulerian multiphase approach a “resolved” CFD-DEM approach can depict the real particle distribution instead of using one mean particle diameter, which is often necessary to reduce computational effort of Eulerian simulations. Further, the DEM captures particle-particle as well as particle-wall contacts at a very detailed physical level and is also capable to include effects of particle shape and surface. This detailed information on particle contacts and particle-fluid interaction allows for developing detailed models for dust generation and transport. Especially in very dense or fixed regimes the DEM clearly outperforms due to its ability to handle steady state solutions.Due to the efficient parallelization of the coupled CFD-DEM method the required simulation times are tolerable – the simulation of 1 second took ~3.5 hours on 20 CPUs with 2.1 GHz and ~150.000 particles.As the calculated results are in good agreement with measurement data, the suggested numerical model seems to be a very promising tool to predict dust generation and propagation. Further work should focus on the development of detailed particle contact based models for dust generation to further increase the accuracy of the model.
Acknowledgement
The authors would like thank the community of CFDEMproject for giving important input and contributions to the development of this open source project. Further we want to thank the Austrian C.D. Research Association, the Federal Ministry of Economy, Family and Youth and the National Foundation for Research, Technology and Development.
■